Skizze:
Das Energiespektrum des Harmonischen Oszillators in der Quantentheorie
Symbole
wie "a" oder "b" können
hintereinandergeschrieben werden, dies gibt den Prototyp einer Multiplikation.
Ignorierbare Klammerung (ab)a=a(ba)=aba bedeutet
Assoziativität der Multiplikation. Die Nichtvertauschbarkeit der Symbole
-- ab und ba sind nicht
gleichbedeutend -- macht die Multiplikation nichtkommutativ. (In der Mathematik
wird die entstandene Struktur "freier Monoid" genannt, generiert durch die
Elemente "a" und "b". )
Die Monoidelemente können addiert werden indem sie um ein "plus"-Zeichen gruppiert werden. Und ein Monoidelement kann mit einer Zahl (komplex oder reel) multipliziert werden, indem diese Zahl vor das betreffende Monoidelement geschrieben wird. Dies ist die Basis um die Heisenberg-Vertauschungsrelation mit Monoiden zu realisieren. (Die Eins repräsentiert das neutrale Element der Monoid-Multiplikation.):
Iterationen entlang der natürlichen Zahlen ergeben:
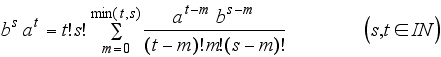
Und das Energie-Eigenwertproblem des eindimensionalen Harmonischen Oszillators kann wie folgt formuliert werden:
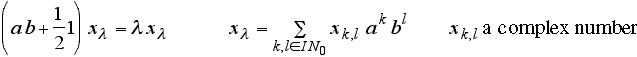
Dieses Problem ist lösbar mit Erweiterungen von Linearkombinationen, die beliebig viele Summanden enthalten können (dies gibt den Begriff der sogenannten "reduzierten Basis" eines Hausdorff-topologischen Vektorraumes, kontrastiert durch die üblicherweise benutzte algebraische Basis eines Vektorraumes (Außerdem ist eine reduzierte Basis etwas gänzlich anderes als die topologische Basis eines Vektorraumes.)). Die Eigenwerte ergeben sich wie erwartet:
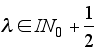
Dies gibt einen neuen Weg zur Lösung des Energieeigenproblems eines Harmonischen Oszillators in der Quantentheorie.