Sketch:
Energy Spectrum of the Quantum Theoretical Oscillator
Symbols
like "a" or "b" can be concatenated
or juxtaposed, giving the prototype of a multiplication. Disrespecting parenthization
(ab)a=a(ba)=aba is called
associativity of the multiplication. Respecting the order of the symbols
ab and ba makes the
multiplication noncommutative. (In mathematics the emerging structure is
called a free monoid generated by the elements "a" and "b". )
The monoid elements can be written as being added by grouping them around a "plus"-sign. And a monoid element can be written as being multiplied by a number (complex or real) by prefixing it with the given number. This is the basis for realizing the Heisenberg commutation-relation with monoids (The one represents the neutral element of the monoid-multiplication.):
Iterations over the natural numbers give:
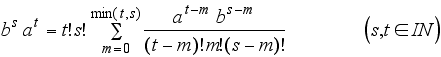
And the energy eigenvalue problem of the one-dimensional harmonic oscillator then can be formulated as follows:
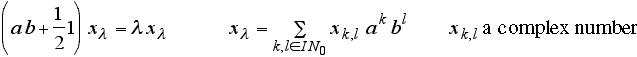
That problem is solved by using extensions of linear combinations to infinitely many summands (giving the notion of the so-called "reduced basis" of a Hausdorff topological vector space as a counterpart to the commonly used algebraic basis of a vector space (Furthermore, the reduced basis is something fundamentally different than a topological basis of a vector space.)). The eigenvalues are as to be expected:
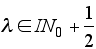
This constitutes a new method of solving the energy-eigenproblem of the harmonic oscillator in quantum theory.